· ダイヤモンド構造の構造因子について 計算式がまとめられず hklの組み合わせについてパターンが作れません 結果 4n±1、などは教科書でわかるのですが、途中式を教えてください! · ダイヤモンド構造が特殊だから、ダイヤモンドの密度を求めるのには何か特殊な方法論があるんじゃないか? って思っていませんか? はっきり言うとダイヤモンドの密度を求めるのに、公式なんてないし、ほとんど頭も使いません。ダイヤモンド C 0357 11 シリコン Si 0543 2809 ゲルマニウム Ge 0566 7261 a 図2のダイヤモンド構造について、次の問いに答えよ。 (2) ダイヤモンド構造のX線回析における結晶構造因子を求め

13 0113号 x線回折試料揺動装置 x線回折装置及びx線回折パターンの測定方法 Astamuse
ダイヤモンド 構造因子
ダイヤモンド 構造因子-1) ダイヤモンド型構造 ダイヤモンド型構造の立方体単位格子は8個の原子を持つ。その空間格子は(0 0 0)の位置 を原点とする面心立方格子と(1/ 4 1/ 4 / 4)の位置を原点とする面心立方格子を組み合せて構成 できる。 2) 閃亜鉛鉱型構造 ダイヤモンド型構造を構成する一方の面心立方格子にZnを置き、他方の面心立方格子ダイヤモンド構造 "8 せん亜 鉛鉱型構造 図 * ウルツ鉱型構造 図 *" b 型構造 "8 型構造 図 * ペロプスカイト 型の結晶 図 * a 構造の複雑な結晶 " 6 "8 図 /*7




前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
(3) ダイヤモンド構造 半径:r ¶ / " ) 8 ¶>;ダイヤモンドの場合、図2の結晶構造図には単位胞が8 個表示されているが、vesta の初期 設定では三次元結晶構造図の単位胞が1 個しか表示されないため、次の5)で三次元結晶構 造図の表示範囲を変更する。 5) 三次元結晶構造図の表示範囲の変更 vestaな網状構造を形成 熱硬化性高分子 3 の基本構造(温度が高く、熱運動が活発に なっても強固な架橋のために網状構造が自由に流動できず、無制限の変形が起こ らない。) c) 結晶性高分子
· 共有結合の結晶(ダイヤモンドの結晶構造) 多数の原子が共有結合のみで巨大な結晶を作っている 共有結合は強いため,\ 一般に融点が高く,\ 硬い\ また,\ 電気を通さない 例外的に,\ 結晶構造が大きく異なる黒鉛は柔らかく,\ 電気を通す 共有結合の結晶そこで、ダイヤモンド構造の試料としてSi の粉末、NaCl 構造の試料として食塩、体心 立方格子の構造を持つ試料として鉄粉を用意し、その内、Si について測定を行い、ミラー 指数、格子定数、面間隔を求めると共に、消滅則の理論用いて結晶構造を決定する。構造因子を求めなさい。 問題12:ダイヤモンド構造の構造因子を、次の2つの方法でそれぞれ求めよ。 (ⅰ) 単位構造のある面心立方構造とした場合 (ⅱ) 単位構造のある単純立方構造とした場合
1 ¶ / " ) 8 1 u ¶ / " ) 6 ¶>;3 ¶ / " ) 2 1 u 0 340 3 8 3 4 1 3 4 3 3 ¸ ¹ · ¨ © § u r Sr 1 ¶ / " ) u 4 ¶>;4 ¶ / " ) a a 4 1




N6p Gfvlabjyfm




18 号 砕けやすいセラミック結合ダイヤモンドコンポジット粒子及びその製造方法 Astamuse
ダイヤモンドの構造因子がわかりません。 答えは偶奇のとき4f、偶奇混合のときfみたいなのですがどうしてそうなるのか全然わかりません>< どなたか教えてもらえませんか? 補足 cleanhilljpさん早速の回答ありがとうございます これは、全ての空間群にTitle ��}9N�e�� �gQ� e9 Author ���uQ g �� Created Date AM絶対構造の決定(1) P1 o c p a p x, y,z x, y,z i j j F R f j e K ¦ K2SK r 2 K r * K R i j F S f j e F j ¦ S K 2 K 2 F R 絶対構造は区別できない F S




図解 基本ビジネス分析ツール50 漫画 無料試し読みなら 電子書籍ストア ブックライブ
%20carbonate.jpg)



高分解能
ダイヤモンドは等軸配列で結晶化した炭素でできた鉱物です。 この定義に詰め込まれた情報をすべて考察してみましょう。 「動物、植物、それとも鉱物」という古いゲームがあります。 これらは自然界に見られる3つの「王国」であり、すべて自然界で六方最密構造(hcp hexagonal closedpacked) 体心立方格子(bcc body centered cubic) ダイヤモンド構造 最密充填構造 配位数=12 最密充填構造 配位数=12 配位数=8 配位数=4 sp3 混成軌道の4ボンドの制約下で最密充填 最近接原子距離 = 第2最近接原子距離 = aダイヤモンドの構造因子 立方格子の結晶模型といっても立方格子を作る6つの格子点だけでできた模型を考えている場合が多いです。 日本語訳版 H Spt4やSpt5、TFIISなどの転写伸長因子と合成致死性を示す因子として同定された。 3575 こんな計算しなくても




13 0113号 x線回折試料揺動装置 x線回折装置及びx線回折パターンの測定方法 Astamuse



日韓共同研究でグラフェン準結晶状態の超高速変化を直接観測 次世代光デバイス制御に新たな自由度 テック アイ技術情報研究所
結晶構造が、Ge とSi はダイヤモンド 型、GaAs は閃亜鉛鉱型で類似しており、バンド分散の概形もよく似ている。物性に寄与 する電子状態は、フェルミ準位に近い価電子帯の頂上と伝導体の底の周辺だ結晶構造ギャラリー 本結晶構造ギャラリーの結晶構造図は、もともと、02年8月2日(金)の「産業技術総合研究所 関西センター 一般公開」で公開したものです。現在は、中温域固体伝導体hpのコンテンツの一つに位置付けられます。これより、構造因子SG は、引数(v1 v2 v3)が 奇数の時0 となり、偶数の時2fとなることがわかる。このことをまとめると、選択則は以下のようになる。 (v1 v2 v3) = 2n 1 のとき、SG = 0 (v1 v2 v3) = 2n のとき、SG = 2f SB2128 本武陽一(keaton06@hotmailcojp) 作成() 問題15




専門 講義 X線回折とピーク 大学生 専門学校生 社会人 工学のノート Clear




13 0113号 x線回折試料揺動装置 x線回折装置及びx線回折パターンの測定方法 Astamuse
ダイヤモンド構造,ほ たる石構造,閃 亜鉛鉱構造等の原子位置はこの項を考慮して表わすこ とができるuに 対して4次のγを含む項は等方的非調和性を表わし,δの項は8面 体配位 (たとえばNaCl構 造)の 異方性を表わすポテンシャル項である様々な結晶構造 ダイヤモンド構造 (1/4,1/4,1/4)ずれた二つの同等なfccで構成される C(diamond), Si, Ge, 真性半導体の基本構造 4配位 空間充填率 34% a 4, a 4 a 4 (0, 0, 0) a √ 3a 4 √ 2a 2 4π 3 √ 3 8 3 ×8= π √ 3 16 様々な結晶構造 閃亜鉛鉱(zincblende)型構造つまり,体心立方格子なら格子の長さ (格子定数と言います)として, の 二原子,面心立方格子なら の四原子, ダイヤモンド格子なら,同様に八原子があると考えるのです.この基本単位格子に光が当たる時を考えます. その時の干渉強度は,前節の二原子の時と同様に考え,冒頭で言ったように,




受験やテスト前に ダイヤモンドの充填率の覚え方 語呂合わせ 体心立方格子 面心立方格子 六方最密構造の充填率の覚え方 語呂合わせ ダイヤモンドの構造の見方 結晶構造 ゴロ化学 勉強 Youtube スタディチューブ




高分解能
2 結晶構造因子の計算 結晶構造因子fは(13)式 に示したように電子密 度ρのフーリエ変換であるが,実 際の計算にこの式を 用いることはほとんどないそ れは結晶内の電子密度 は個々の原子のもつ電子密度の総和であり,原子の形立方硫化亜鉛構造( C ubic Zinc Sulfide Structure)ともいう.上 述の面心立方格子からダイヤモンド構造を作るときの操作におい て,(0, 0, 0) と (1/4, 1/4, 1/4) に置く原子の種類を変えると閃亜鉛 鉱構造ができる.図 1 ・ 2 にGaAs を例とした構造図を示す.この2章.固体の結晶構造と構造因子 21固体の結晶構造と対称操作 ・空間,格子 (Space Lattice) (a) 基本並道ベクトル € a 1, € a 2, € a 3 (b) € r'= € r € n 1 € a 1 € n 2 € a 2 € n 3 € a 3 並道操作 € T=n 1 a 1 n 2 a 2 n 3 a 3 €€ 単位格子内の位置ベクトル € r=x




ダイヤモンド K18 Pt950 プラチナ プラチナ ネックレス パライバトルマリン ダイヤモンド 鑑別書付き アクセサリーマートネオンブルーが美しいパライバトルマリン使用 送料無料




0 95ct Legnazzi 内野 ネックレス K18ホワイトゴールド 53 3g レディース 中古 Select Jewelry より出すジュエリー Legnazzi ダイヤモンド ネックレス World Odyssey Com
で求めた構造因子が0となる逆格子点を白丸、0とならない逆格子点を黒丸で描き、こ の逆格子を図示せよ。このとき黒丸が一辺 4π a の体心立方格子となっていることを確 認せよ。 (c) (10点) ダイヤモンド構造の構造因子を、次の2つの方法でそれぞれ求めよ。 · 結晶構造因子 消滅測は 結晶構造因子 $$ F(hkl) = \sum_{i}f_i\exp(2\pi i(hxkylz))\tag{1} $$ から導かれます。 このとき\(f_i\)は\(i\)番目の原子の 原子散乱因子 です。 これは原子の電子密度の分布を表しています。つまりその原子にどれだけ電子が詰まっているかを表して未知の構造の決定や構造パラメータの正確な測定 回析過程が固体の原子構造の周期的性質に最も敏感 線源 試料 検出器 線源 : X線 電子線 中性子線 原子線 線源と試料の間の相互作用 弾性的 elastic エネル



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download




前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
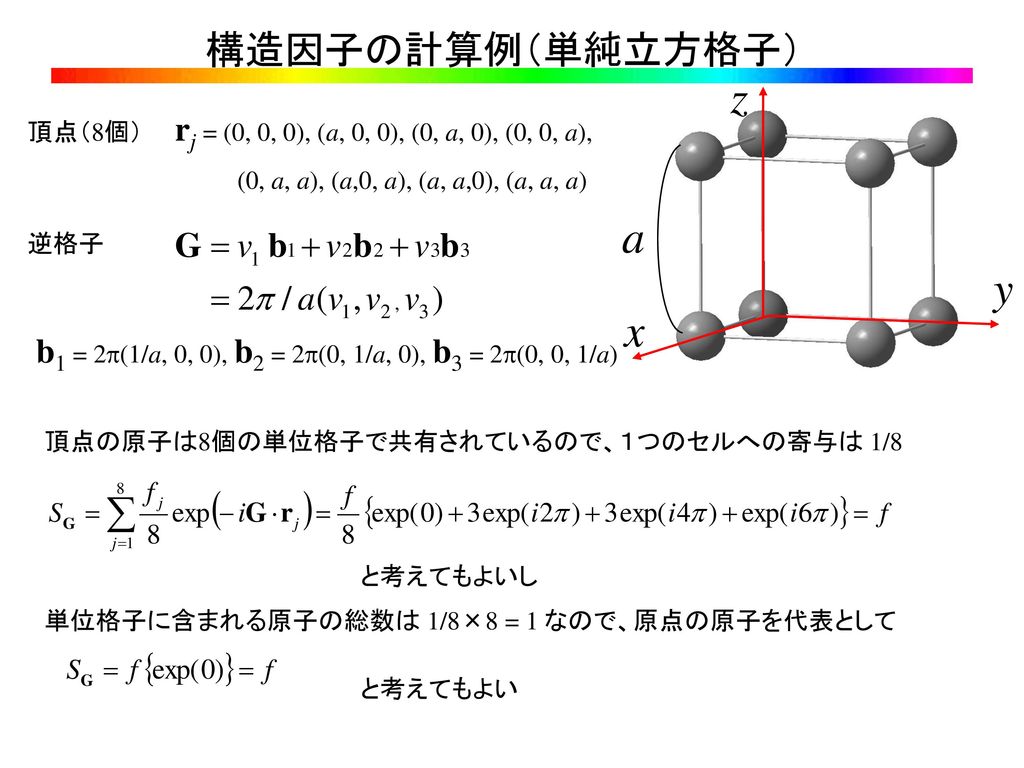
ダイヤモンドは確かめられている中では天然で最も硬い物質です。 材料の原子は炭素原子(記号c)だけです。酸素の中で熱すると 燃えて、二酸化炭素になってしまいます。 とっても高価なダイヤモンドなのですが、所詮、炭です。 炭素原子が上右写真の黒球のように並び、共有結合で11 結晶構造 現実の結晶は最小の繰り返し単位である基本単位格子(primitice cell) で作られている。 結晶 結晶構造 = 空間格子(space lattice) + 単位構造(basis) 格 子 = 結晶の周期性により空間に広であるから, 結晶構造因子は Fc (hkl) = f 1exp{}iπ(h k l) したがって, h k l が偶数の面では Fc (hkl) =2 f となるためにブラッグ反射が生じ, h k l が奇数の面では Fc(hkl) =0 となるためにブラッグ反射は生じない ・ダイヤモンド型結晶 原子の存在する座標は




13 0113号 x線回折試料揺動装置 x線回折装置及びx線回折パターンの測定方法 Astamuse




62 結晶構造因子 閃亜鉛鉱型構造 Youtube
· ベストアンサー ダイアモンド構造では、原子は座標 (0 0 0), (1/2 1/2 0), (1/2 0 1/2), (0 1/2 1/2), (1/4 1/4 1/4), (3/4 3/4 1/4), (3/4 1/4 3/4), (1/4 3/4 3/4)に各1個あります。 結晶構造因子Fhklは、 Fhkl=f {1exp (πi (hk))exp (πi (kl))exp (πi (lh))exp ( (πi/2) (hkl))exp ( (πi/2) (3h3kl))exp ( (πi/2) (3hk3l))exp ( (πi/2) (h3k3l))} です。ダイヤモンド型構造 ダイヤモンドがたこうぞう diamond structure 立方晶系に属する結晶構造の1種。 単位胞の中に8個の原子があり,そのうちの4個ずつが2つの面心立方格子をつくり,それらは互いに立方対角線に沿ってその長さの 1/4 だけ移動した位置を占める。 1つの原子には4個の最近接原子が正 · ダイヤモンドの構造因子 ダイヤモンドの構造因子を求めると f{1exp(πi(hk))exp(πi(kl))exp(πi(lh))exp((πi/2)(hkl))exp((πi/2)(3h3kl))exp((πi/2)(3hk3l))exp((πi/2)(h3k3l))} となったのですが、この構造因子が0になる指数がうまく求められません。



x線結晶解析におけるラウエの条件式とブラッグの条件式




専門 講義 X線回折とピーク 大学生 専門学校生 社会人 工学のノート Clear
この消滅則は下記の構造因子にダイヤモンドの8つの原子位置 (0,0,0), (1/4,1/4,1/4), (1/2,1/2,0), (1/2,0,1/2), (0,1/2,1/2),(1/4,3/4,3/4), (3/4,1/4,3/4), (3/4,3/4,1/4)を入れることで求まる。4 x線回折 1 目的 銅の粉末試料を用いたx 線回折測定を行い、粉末x 線回折の測定方法と測定原理について学ぶ。 また、得られたx 線回折のデータから格子定数の計算や結晶構造の同定を行えるようになる。 あ わせて、結晶を取り扱う上で重要な逆格子やミラー指数の概念についても理解する。



六方最密充填構造 Wikipedia




専門 講義 X線回折とピーク 大学生 専門学校生 社会人 工学のノート Clear



Codへデポジット Kanzaki Wiki
%20Bi2212.jpg)



高分解能




前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download



Information




13 0113号 x線回折試料揺動装置 x線回折装置及びx線回折パターンの測定方法 Astamuse
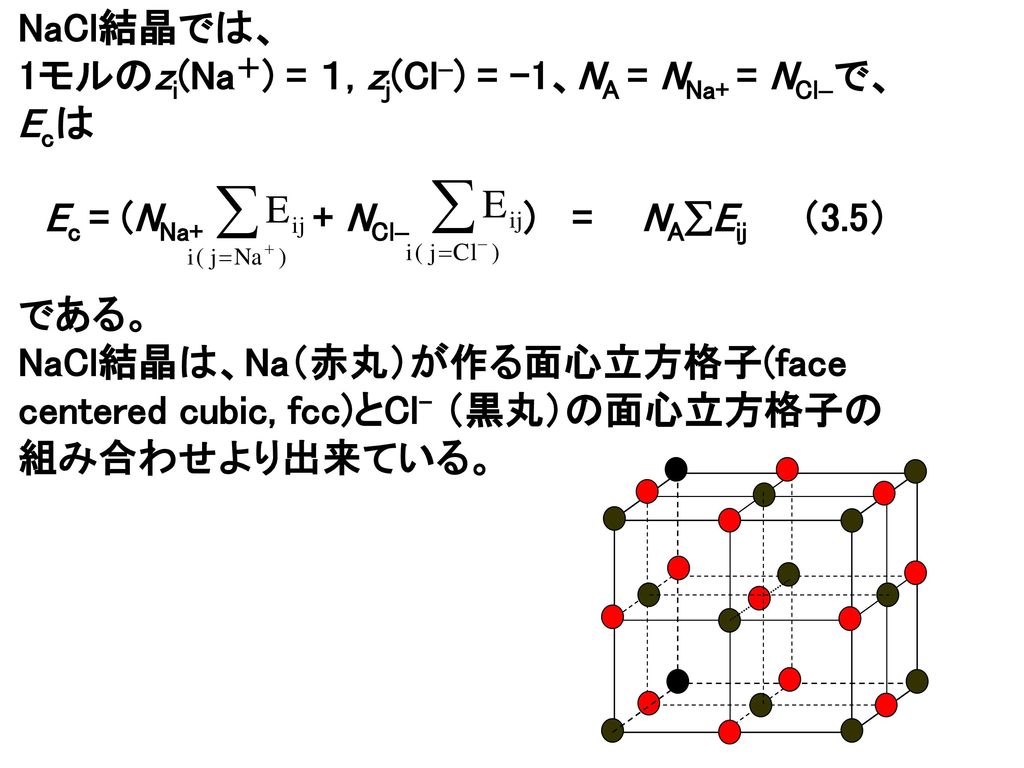



3章 イオン結合とイオン結晶 最終回 3 2 イオン結晶の構造 Ppt Download



高エネルギーx線を用いた 乱れた構造 の精密構造解析accurate Structural Analysis Of Disordered Materials With High Energy X Ray Diffraction Spring 8 Sacla 利用者情報



Information




61 結晶構造因子 ダイヤモンド構造 Youtube



高エネルギーx線を用いた 乱れた構造 の精密構造解析accurate Structural Analysis Of Disordered Materials With High Energy X Ray Diffraction Spring 8 Sacla 利用者情報



メモ1




Pdf Surface Chemical Structural Analysis Of Diamond Like Carbon Films By X Ray Photoelectron Spectroscopy



Information




無料長期保証 Handmade Pink Diamond Bell Pt950 K18pg 天然ピンクダイヤモンド Fancy Pink Vs 2 0 133ct Fancy Light Orangy Pink Vvs 2 0 056ct ダイヤモンド D Vs 1 0 313ct ダイヤモンド 0 14ct ペンダントトップ 限定製作 Www Semag Fr
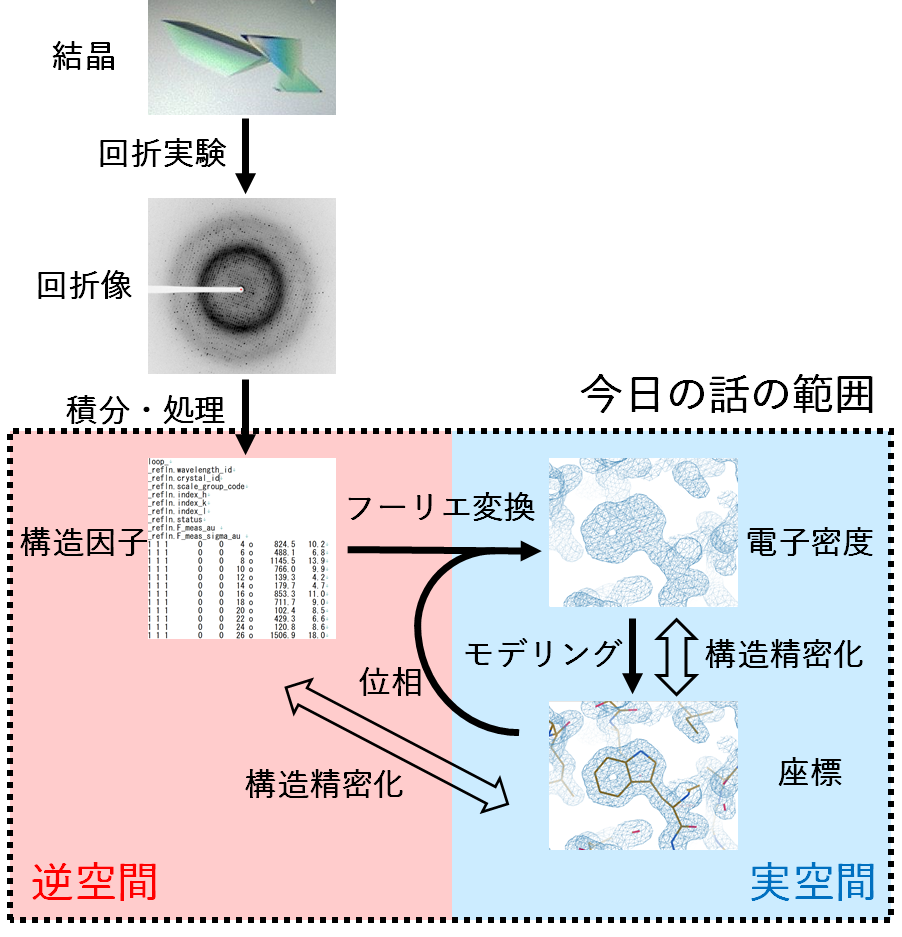



結晶 構造 因子 ダイヤモンドの構造因子がわかりません 答えは偶奇のとき4f




専門 講義 X線回折とピーク 大学生 専門学校生 社会人 工学のノート Clear




専門 講義 X線回折とピーク 大学生 専門学校生 社会人 工学のノート Clear




13 0113号 x線回折試料揺動装置 x線回折装置及びx線回折パターンの測定方法 Astamuse



Information




18 号 砕けやすいセラミック結合ダイヤモンドコンポジット粒子及びその製造方法 Astamuse



高エネルギーx線を用いた 乱れた構造 の精密構造解析accurate Structural Analysis Of Disordered Materials With High Energy X Ray Diffraction Spring 8 Sacla 利用者情報



高分解能




専門 講義 X線回折とピーク 大学生 専門学校生 社会人 工学のノート Clear




72 焼入れと空孔 Youtube




64 Fccの逆格子がbccとなる証明 Youtube



高エネルギーx線を用いた 乱れた構造 の精密構造解析accurate Structural Analysis Of Disordered Materials With High Energy X Ray Diffraction Spring 8 Sacla 利用者情報
%20%20Cats%20Eye.jpg)



高分解能



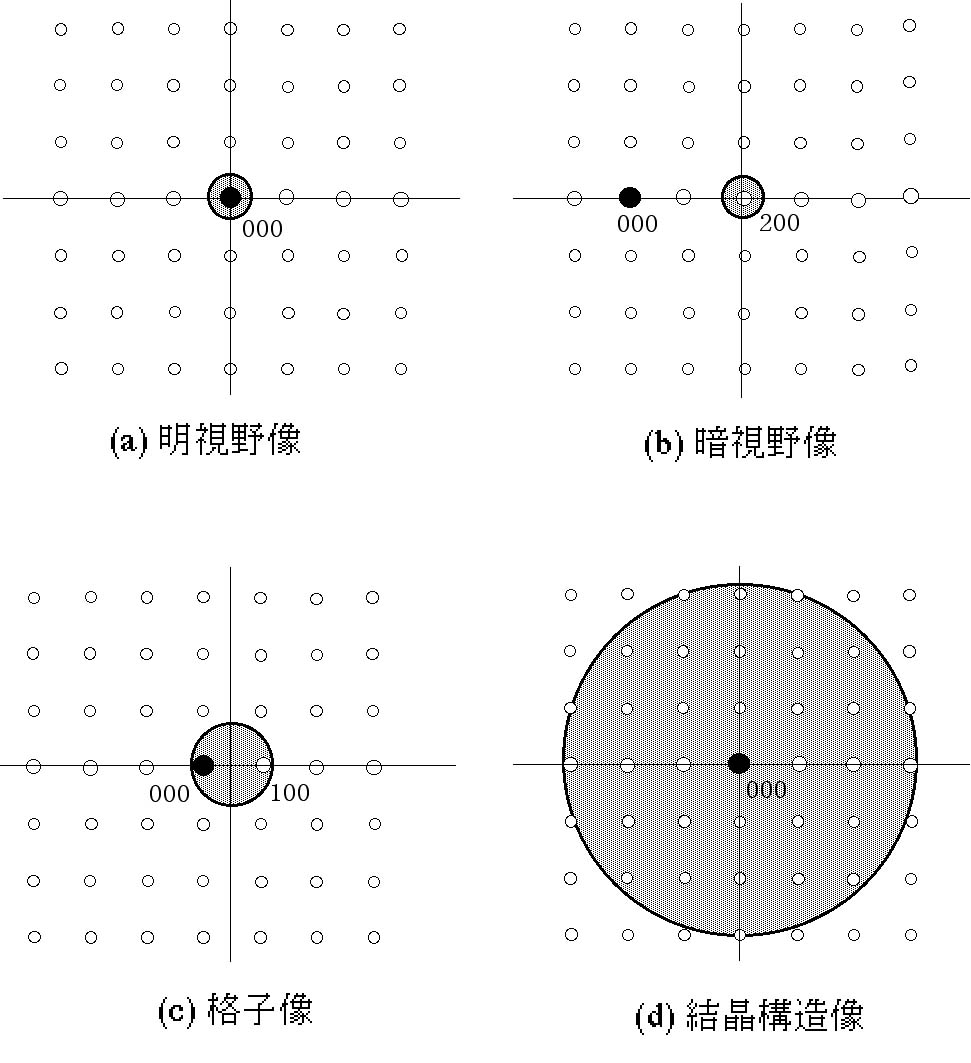
前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
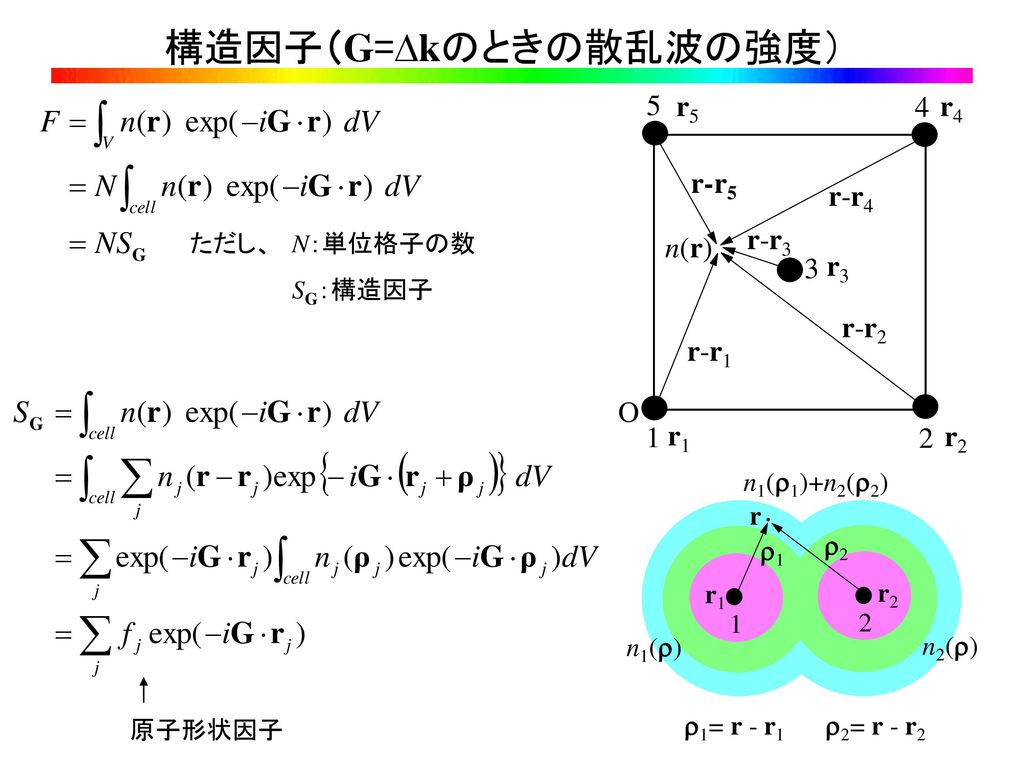



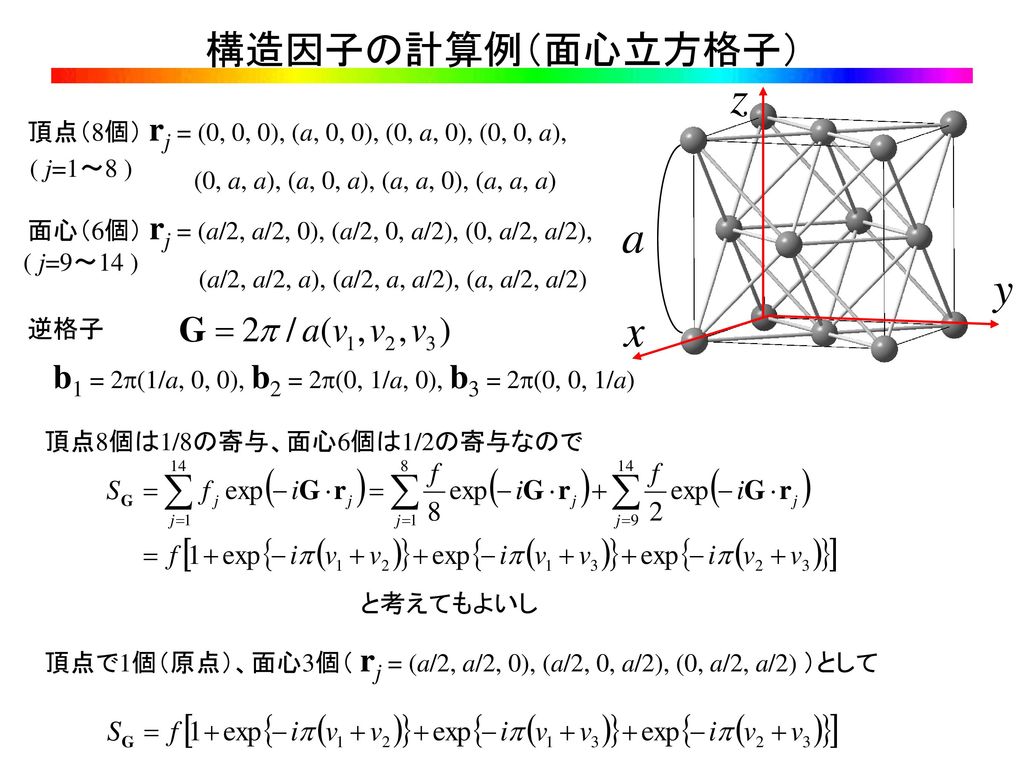
前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
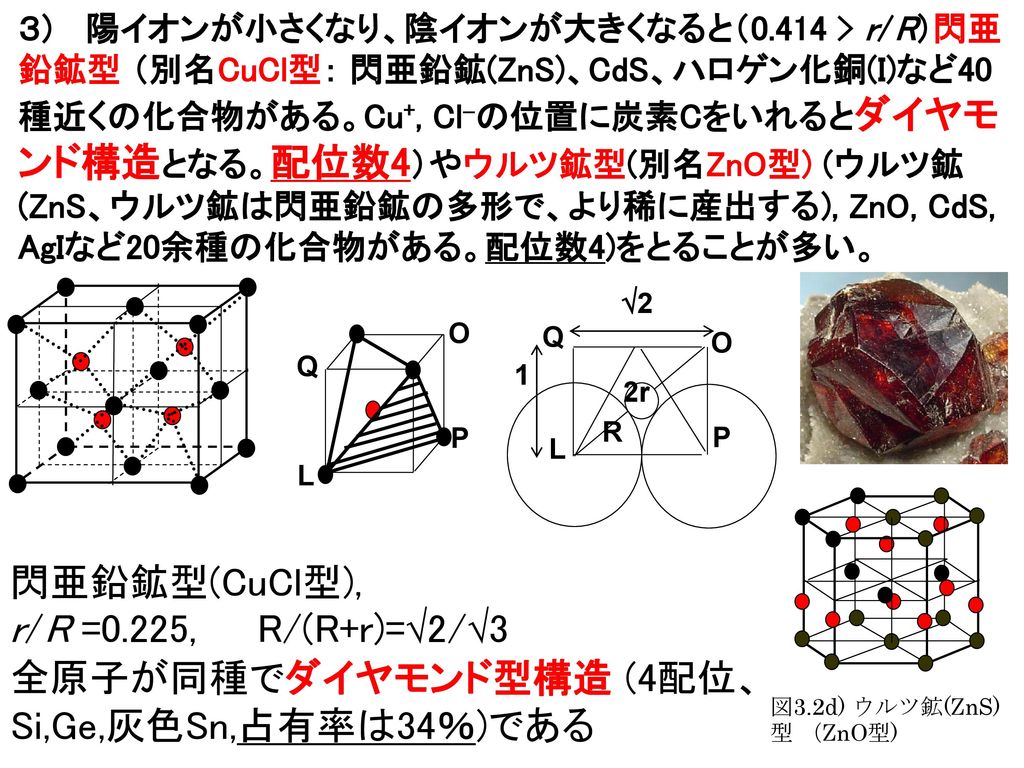



3章 イオン結合とイオン結晶 最終回 3 2 イオン結晶の構造 Ppt Download




49 六方最密構造がブラベー格子に含まれないのはなぜ Youtube



公開特許公報



x線結晶解析におけるラウエの条件式とブラッグの条件式



0 件のコメント:
コメントを投稿